高二数学立体几何试题

　　二. 填空题(每小题4分，共16分)

　　13. 正方体的全面积是 ，它的顶点都在球面上，这个球的表面积是__________。

　　14. 正四棱台的斜高与上、下底面边长之比为5：2：8，体积为 ，则棱台的高为____________。

　　15. 正三棱柱的底面边长为a，过它的一条侧棱上相距为b的两点作两个互相平行的截面，在这两个截面间的斜三棱柱的侧面积为____________。

　　16. 已知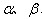是两个不同的平面，m、n是平面 之外的两条不同的直线，给出四个论断：

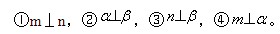
　　以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题______________。

　　三. 解答题(共74分)

　　17. (12分)正方体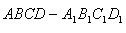中，E、F、G分别是棱DA、DC、^DD1的中点，试找出过正方体的三个顶点且与平面EFG平行的平面，并证明之。

　　18. (12分)球内有相距1cm的两个平行截面，截面的面积分别是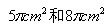，球心不在截面之间，求球的表面积与体积。

　　19. (12分)一个正三棱柱的三视图如图所示，求这个正三棱锥的表面积。

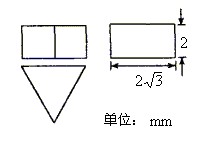
　　20. (12分)直角梯形的一个内角为45°，下底长为上底长的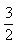，这个梯形绕下底所在直线旋转一周所成的旋转体的全面积是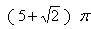，求这个旋转体的体积。

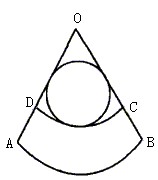
　　21. (12分)有一块扇形铁皮OAB，∠AOB=60°，OA=72cm，要剪下来一个扇形ABCD，作圆台形容器的侧面，并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面)。(如图)试求

　　(1)AD应取多长?

　　(2)容器的容积。

　　22. (14分)如图，正四棱柱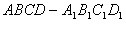中，底面边长为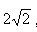，侧棱长为4，E、F分别为AB、BC的中点，。

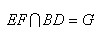　　(1)求证：平面 ;

　　(2)求点 到平面 的距离d;

　　(3)求三棱锥 的体积V。

　　高二数学立体几何需要童鞋们有较强的空间思维能力，所以高二的童鞋们要想学好高二数学立体几何就需要多做立体几何方面的练习题，从练习题中提升自己对问题的掌握。在此www.67xuexi.com小编祝大家在考试中都能取得好成绩！

上一页  [1] [2]