三角函数诱导公式概念、知识点及练习题
[10-20 18:10:12] 来源:http://www.67xuexi.com 高二数学 阅读:85387次
同理,两式相减我们就得到sina*sinb=-[cos(a+b)-cos(a-b)]/2
这样,我们就得到了积化和差的公式:
cosa*sinb=[sin(a+b)-sin(a-b)]/2
sina*sinb=-[cos(a+b)-cos(a-b)]/2
好,有了积化和差的四个公式以后,我们只需一个变形,就可以得到和差化积的四个公式.
我们把上述四个公式中的a+b设为x,a-b设为y,那么a=(x+y)/2,b=(x-y)/2
把a,b分别用x,y表示就可以得到和差化积的四个公式:
sinx+siny=2sin[(x+y)/2]*cos[(x-y)/2]
sinx-siny=2cos[(x+y)/2]*sin[(x-y)/2]
cosx+cosy=2cos[(x+y)/2]*cos[(x-y)/2]
cosx-cosy=-2sin[(x+y)/2]*sin[(x-y)/2]
www.67xuexi.com四、三角函数
同角三角函数的基本关系式
倒数关系
tanα ·cotα=1
sinα ·cscα=1
cosα ·secα=1
商的关系
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
平方关系
sin^2(α)+cos^2(α)=1
1+tan^2(α)=sec^2(α)
1+cot^2(α)=csc^2(α)
同角三角函数关系六角形记忆法
构造以"上弦、中切、下割;左正、右余、中间1"的正六边形为模型。
倒数关系
对角线上两个函数互为倒数;
商数关系
六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系。)。由此,可得商数关系式。
平方关系
在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
两角和差公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tan(α+β)=(tanα+tanβ )/(1-tanα ·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα ·tanβ)
二倍角的正弦、余弦和正切公式
sin2α=2sinαcosα
cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan2α=2tanα/(1-tan^2(α))
tan(1/2*α)=(sin α)/(1+cos α)=(1-cos α)/sin α
半角的正弦、余弦和正切公式
sin^2(α/2)=(1-cosα)/2
cos^2(α/2)=(1+cosα)/2
tan^2(α/2)=(1-cosα)/(1+cosα)
tan(α/2)=(1—cosα)/sinα=sinα/1+cosα
万能公式
sinα=2tan(α/2)/(1+tan^2(α/2))
cosα=(1-tan^2(α/2))/(1+tan^2(α/2))
tanα=(2tan(α/2))/(1-tan^2(α/2))
三倍角的正弦、余弦和正切公式
sin3α=3sinα-4sin^3(α)
cos3α=4cos^3(α)-3cosα
tan3α=(3tanα-tan^3(α))/(1-3tan^2(α))
三角函数的和差化积公式
sinα+sinβ=2sin((α+β)/2) ·cos((α-β)/2)
sinα-sinβ=2cos((α+β)/2) ·sin((α-β)/2)
cosα+cosβ=2cos((α+β)/2)·cos((α-β)/2)
cosα-cosβ=-2sin((α+β)/2)·sin((α-β)/2)
三角函数的积化和差公式
sinα·cosβ=0.5[sin(α+β)+sin(α-β)]
cosα·sinβ=0.5[sin(α+β)-sin(α-β)]
cosα·cosβ=0.5[cos(α+β)+cos(α-β)]
sinα·sinβ=- 0.5[cos(α+β)-cos(α-β)]
【练习题】
1.如果|cosx|=cos(x+π),则x的取值集合是( )
A.-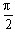 +2kπ≤x≤
+2kπ≤x≤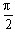 +2kπ B.-
+2kπ B.-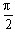
- 上一篇:平面向量概念、知识点及练习题