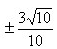任意角的三角函数概念、知识点及练习题

　　【概念及知识点】

　　任意角三角函数

　　在任意角三角形中，各边角有以下的函数关系：

　　正弦定理 在任意角三角形中，各个角的正弦与它所对的边的比相等，并且等于外接圆的直径。

　　余弦定理 在任意角三角形中，任意一边的平方等于其余两边的平方和减去这两边的乘积的两倍与它们的夹角的余弦的积。

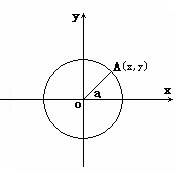
　　在直角坐标系中,⊙O的半径为1,任意角α的三角函数定义如下:

　　正弦:∠α与单位圆的交点A的纵坐标与圆半径的比值叫做正弦,表示为:sinα=Ay/OA=Ay;其中Ay 叫做正弦线。

　　余弦: ∠α与单位圆的交点A的横坐标与圆半径的比值叫做余弦,表示为:cosα=Ax/OA=Ax;其中Ax 叫做余弦线。

　　正切: ∠α与单位圆的交点A的纵坐标与横坐标的比值叫做正切,表示为:tanα=Ay/Ax;

　　余切: ∠α与单位圆的交点A的横坐标与纵坐标的比值叫做余切,表示为:cotα=Ax/Ay; ;

　　正割: 圆半径和∠α与单位圆的交点A的横坐标的比值叫做正割,表示为:secα=OA/Ax=1/Ax;

　　余割: 圆半径和∠α与单位圆的交点A的纵坐标的比值叫做余割,表示为:cscα=OA/Ay=1/Ay;

　　【练习题】

　　1.若角a的终边过点(-3，-2)，则(　)

　　A.sina tana>0 B.cosa tana>0 C.sina cosa>0 D.sina cota>0

　　2.使lg(cosθ·tanθ)有意义的角θ是(　　)

　　A.第一象限角 B.第二象限角

　　C.第一或第二象限角 D.第一、二象限角或终边在y轴上

　　3.已知角a的终边落在直线y=3x上，则sina=________.

　　【答案】

　　1、C

　　2、C

　　3、